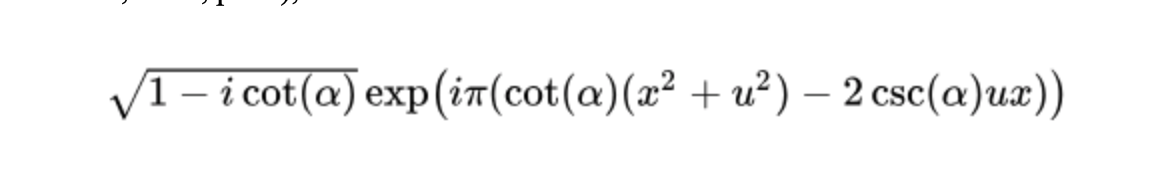This brief report introduces the fractional Fourier transform (FRFT). The analysis
first discusses the nature and fundamental properties of the transform. It then explores how the
technique can favorably be applied toward the solution of a practical problem in mathematical
physics.
The fractional Fourier transform is a family of linearizing integral transforms that represent a
generalization of the well-known Fourier transform. It is not unreasonable to think of the FRFT as a
“Fourier transform to the nth power,” where n is a fraction between zero and one.
Consequently, it represents the re-characterization of a function to a domain that is somehow intermediate between the time domain (for which n = 0) and the frequency domain (for which n = 1). Like any integral transform, the overarching concept of the transform is its ability to map a physical situation governed by differential equations from a domain in which it is difficult to solve into another domain in which it is more readily analyzed. Like the Fourier transform, the FRFT—at least in part—is capable of representing a driving function, such as a Green’s function (Narayanan & Prabhu, 2003, p. 511), in terms of an independent orthonormal basis that enables differential equations in which it is involved to be solved by superposition of the effects of individual components in the transformed domain. Naturally, transformed functions in the fractional Fourier domain must possess the same spectral energy that they possess in the time domain, consistent with and obedient of Parseval’s theorem.
The FRFT exhibits similar behavioral properties to the original Fourier transform. That is to say, it is subject to linear superposition, scaling, shifting in time, shifting in frequency, and various types of symmetry. It also demonstrates a number of unique properties, including the mixed product rule and the exponential rule (McBride & Kerr, 1987, p. 172). The FRFT differs from the Fourier transform because its kernel function, rather than a pure sinusoid (Alieva & Bastiaans, 2003, p. 27), is formed as:
in the most general case and by a Dirac delta function in the case where α is a multiple of π.
Local fractional calculus can be applied to non-differentiable functions applied over any fractional space. This makes the local fractional Fourier transform an ideal candidate for treating fractal signal functions. It also demonstrates that, consistent with the Mittag-Leffler function, semi-group properties are applicable across all fractal sets. Concomitantly, uncertainly principles that can be derived from local fractional Fourier analysis indicate that the fractional Schrodinger equation—which derives from the de Broglie and Planck-Einstein relations—can be represented in fractal space-time with marked facility. In particular, the FRFT can directly solve the local fractional Schrodinger equation. Note first that the equation can be represented by the superposition of a set of fractal plane waves. If a number of atoms are independently studied, their respective states, measured independently, can ostensibly be described by identical wave functions. The result of a position measurement, then, can be characterized as a fractal probability density, the set of impacts of which is distributed in space according to another density function. Any set of N measurements can be described by am expectation value and a mean-squared dispersion.
Now, the physical interpretation of a particle in fractal space is a certain probability that involves gamma functions, the integral of which over all fractal space can be evaluated in concert with the Rayleigh-Jeans law. Application of the FRFT permits the fractal mechanical operator to be expressed in closed form as a sum of an infinite number of integrals (Yang et al., 2013, pp. 11-14).
References Alieva, T., & Bastiaans, M. J. (2003). Fractional cosine and sine transformations. Asian Journal of Physics 12(1): 25-32. McBride, A. C., & Kerr, F. H. (1987). On Namias’s fractional Fourier transformation. IMA Journal of Applied Mathematics 39: 159-175. Narayanan, V. A., & Prabhu, K. M. M. (2003). The fractional Fourier transform: Theory, application and error analysis. Microprocessors and Microsystems 27: 511-521. Yang, X.-J., et al. (2013). Mathematical aspects of the Heisenberg uncertainty principle within local fractional Fourier analysis. Boundary Value Problems 2013: 1-16. Retrieved from https://core.ac.uk/download/pdf/81901191.pdf.